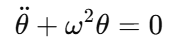Before we dive into the concept of stability, it is important to first understand what is meant by a dynamic system.
A dynamic system is a system whose state or output changes over time, usually influenced by initial conditions and inputs. Examples are wide-ranging, ranging from mechanical systems (such as pendulums) to electronic systems (such as RLC circuits) to biological and economic systems.
Dynamic systems are typically modeled using differential equations, or difference equations. These models allow us to analyze how the system reacts to various inputs and disturbances over time.
What is Dynamic System Stability?
In simple terms, system stability is the property of a system to return to equilibrium after a small disturbance.
Imagine a ball placed at the bottom of a bowl. If we push the ball slightly, it will oscillate for a moment and then return to its equilibrium point. This is an example of a stable system.
Conversely, if the ball is placed at the top of a small hill, even the slightest push will cause the ball to move away from its starting point without returning. This is an example of an unstable system.
In the context of mathematics and engineering, system stability has a more formal meaning depending on the type of system (continuous or discrete), but it generally falls into two main categories:
Asymptotic Stability: The system not only remains close to the equilibrium point, but also approaches it over time.
Lyapunov Stability: The system remains in a neighborhood around the equilibrium point if it starts close enough to it.
Why is Stability Important?
In the real world, systems are always exposed to disturbances. These disturbances can come from the environment, model uncertainty, or input variations. If the system is unstable, even a small disturbance can cause major damage, loss of control, or even total failure.
For example:
- In autonomous vehicle control, stability is critical to prevent vehicles from veering off course.
- In economics, financial system stability is critical to prevent crises and hyperinflation.
In electric power systems, frequency and voltage stability are crucial to prevent total blackouts.
How to Determine System Stability?
There are various methods used to analyze the stability of dynamic systems, depending on whether the system is linear or nonlinear, continuous or discrete.
1. Eigenvalue Analysis (Linear Systems)
For linear systems, the most common approach is to analyze the state matrix (A) of the system. If the system is expressed in the form:
then stability is determined by the eigenvalues of the matrix A. The system is stable if all eigenvalues have negative real parts.
Example:
- If all eigenvalues of A are -1, -2, and -3 → the system is stable.
- If one of the eigenvalues is +0.5 → the system is unstable.
2. Transfer Function and Pole Location (Linear Continuous System)
For a system represented by a transfer function:
Stability is determined by the location of the poles of the system (the roots of D(s)). If all the poles are to the left of the imaginary axis (Re(s) < 0), then the system is stable.
3. Routh-Hurwitz Criterion
Is an algebraic method used to determine the stability of a linear system without directly calculating the roots of the characteristic polynomial.
This method constructs a Routh table of polynomial coefficients and checks the sign of the first row. If all are positive, the system is stable.
4. Nyquist and Bode Criteria (Frequency Analysis)
Used to analyze the stability of linear systems in the frequency domain. Suitable for feedback systems.
The Nyquist criterion observes the trajectory of the Nyquist plot and how it circles the critical point (-1,0). If the number of circles matches the number of poles on the right, the system is considered stable.
5. Lyapunov Function (Nonlinear Systems)
For nonlinear systems, the eigenvalue approach is no longer sufficient. This is where the Lyapunov method comes in.
The Lyapunov function is a scalar function
𝑉(𝑥)> 0 for all x not same 0
V˙(x)<0 for all x not same 0
6. Simulation and Numerical Analysis
In practice, especially for complex or nonlinear systems, numerical approaches such as simulations using MATLAB, Simulink, or Python (SciPy) are used to visualize the system response to disturbances.
Responses such as step responses, impulse responses, or real-time simulations can provide an intuitive indication of whether the system is stable or not.
Simple Case Example
Imagine a small frictionless linear pendulum system:
This model has a harmonic oscillation solution. The system is marginally stable because it does not drift, but it also does not return to its initial position exponentially.
However, if damping is added:
with ζ>0, then the system becomes asymptotically stable.
Conclusion
The stability of dynamic systems is one of the fundamental aspects in the design and analysis of systems in various fields. Without stability, the performance and reliability of the system are questionable.
In linear systems, stability can be determined by fairly direct mathematical approaches, such as eigenvalue analysis or the Routh-Hurwitz criterion. For nonlinear systems, approaches such as the Lyapunov function or numerical simulation are required.
By understanding and being able to analyze stability, we can design safer, more reliable, and more efficient systems.