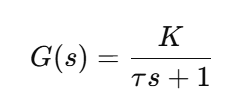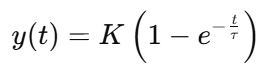Analisis Sistem Orde 1 dan Orde 2: Karakteristik, Grafik, dan Contoh

 

Dalam dunia teknik, khususnya di bidang kontrol dan sistem dinamik, pemahaman terhadap sistem orde 1 dan orde 2 sangat penting. Dua jenis sistem ini merupakan blok bangunan dasar dalam pemodelan dan analisis sistem fisis, seperti rangkaian listrik, sistem mekanik, dan proses industri.

Artikel ini akan membahas:

• Apa itu sistem orde 1 dan orde 2
• Karakteristik umum masing-masing sistem
• Grafik respons terhadap masukan
• Contoh penerapan dalam dunia nyata

Apa Itu Sistem Orde 1 dan Orde 2?

• Sistem orde 1 adalah sistem dinamis yang memiliki satu elemen penyimpan energi (misalnya kapasitor atau induktor), atau satu turunan pertama dalam persamaan diferensialnya.
• Sistem orde 2 memiliki dua elemen penyimpan energi atau dua turunan dalam persamaan diferensialnya.

Biasanya sistem ini dimodelkan menggunakan fungsi alih (transfer function) dalam domain Laplace.

Sistem Orde 1

Bentuk Fungsi Alih:

• K = gain (penguatan sistem)

• $\tau$ = konstanta waktu (time constant)

Karakteristik Utama:

• Respons terhadap masukan tangga (step):

• Sistem akan mencapai sekitar 63,2% dari nilai akhirnya dalam waktu $\tau$.
• Tidak memiliki overshoot atau osilasi.
• Stabil jika $\tau > 0$.

Contoh Sistem Orde 1:

• Pengisian kapasitor dalam rangkaian RC
• Termometer merkuri dalam suhu ruangan (respon suhu)

Sistem Orde 2

Bentuk Fungsi Alih:

• ωn​ = frekuensi alami (natural frequency)
• $\zeta$ = rasio redaman (damping ratio)

Klasifikasi Berdasarkan Redaman:

$\mathrm{-\; \zeta }>\mathrm{1\; :\; overdamped}$

- ζ=$1$: critically damped

- $0<\zeta <1$: underdamped

- $\zeta =0$: undamped (osilasi murni)

Karakteristik Utama (Underdamped):

• Memiliki overshoot, osilasi, dan waktu naik (rise time) yang khas
• Nilai maksimum pertama melebihi nilai akhir
• Mencapai kestabilan setelah beberapa siklus

Parameter Penting:

• Overshoot (OS):

Waktu penetapan (settling time):

$$$$

Sistem Orde 1: Sederhana Tapi Penting

Contoh Paling Umum:

Bayangkan kamu mengisi air dalam ember dengan keran. Level air naik secara bertahap. Proses ini bisa digambarkan oleh sistem orde 1.

Fungsi Alih:

• K: Penguatan (gain)
• τ: Konstanta waktu

Sifat-Sifat Sistem Orde 1:

-Tidak memiliki osilasi

- Responsnya ekponensial

 - Semakin besar 

- τ, semakin lambat sistem merespons

- Stabil jika τ>0τ>0

Respons Step:

Jika diberi masukan berupa “step” (misalnya tegangan mendadak), respons sistem:

Artinya, dalam waktu $\approx 5\tau$, sistem sudah hampir mencapai nilai akhirnya.

Contoh Aplikasi:

• Termometer digital (membutuhkan waktu untuk menstabilkan suhu)
• Rangkaian listrik RC
• Proses pemanasan air

Sistem Orde 2: Kompleks, Realistis, dan Menarik

Sistem ini lebih realistis karena banyak sistem di dunia nyata bersifat berosilasi.

Fungsi Alih:

• ωn​: Frekuensi alami
• $\zeta$: Rasio redaman

Tipe-Tipe Respons Sistem Orde 2:

Nilai $\zeta$	Tipe Redaman	Perilaku
0	Tak teredam	Osilasi terus-menerus
0 < $\zeta$ < 1	Underdamped	Osilasi meredam
1	Critically damped	Cepat, tanpa osilasi
>1	Overdamped	Lambat, tanpa osilasi

Parameter Penting:

• Overshoot → Seberapa tinggi lonjakan melebihi target
• Waktu naik (rise time) → Seberapa cepat sistem mulai naik
• Waktu penetapan (settling time) → Kapan sistem dianggap stabil

Contoh Aplikasi:

• Sistem suspensi kendaraan
• Servo motor
• Rangkaian listrik RLC

Kenapa Harus Paham Ini?

Mengetahui perbedaan sistem orde 1 dan 2 membantu kita dalam:

• Mendesain sistem kontrol (seperti PID)
• Memilih sensor dan aktuator
• Menyusun simulasi yang akurat dalam MATLAB/Simulink

Penutup

Analisis sistem orde 1 dan orde 2 adalah fondasi utama dalam dunia teknik sistem dan kontrol. Pemahaman konsep ini akan membuka pintu untuk desain sistem yang lebih kompleks di masa depan—baik di industri otomotif, robotik, hingga pengolahan sinyal.

Punya pertanyaan atau ingin tahu bagaimana mensimulasikannya dengan MATLAB atau Python? Tulis di komentar atau hubungi kami!

$$G(s) = \frac{\omega_n^2}{s^2 + 2\zeta \omega_n s + \omega_n^2}$$