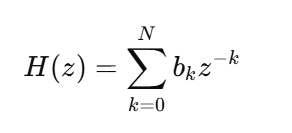Digital Filters & Impulse Response: The Relationship Between FIR, IIR, and System Response

 In the world of digital signal processing (DSP), digital filters play a central role in a variety of applications, from voice processing, images, to digital communications. The two most commonly used types of digital filters are FIR (Finite Impulse Response) and IIR (Infinite Impulse Response). Both have unique characteristics and are used in different contexts, depending on the needs of the system.

This article will thoroughly discuss the relationship between digital filters, impulse responses, and the fundamental differences and relationships between FIR and IIR. By understanding this relationship, we can more accurately select or design the appropriate filter in real implementations.

1. What is a Digital Filter?

In general, a digital filter is a system that converts a digital input signal into an output signal in a certain way, such as eliminating noise, highlighting certain frequencies, or limiting the frequency range of the signal.

In DSP, a digital filter is represented as a linear and time-invariant (LTI) system that can be described through an impulse response and transfer function.

2. Impulse Response: The Foundation of LTI Systems

What is Impulse Response?

Impulse response is the output of a system when given a unit impulse (Dirac delta) input. In digital systems, a unit impulse is denoted as:

The system output to this input is called the impulse response and is denoted by 

ℎ[𝑛]. The impulse response is the key to understanding the characteristics of digital systems.

Relationship With Convolution

One of the advantages of LTI systems is that the output for any input can be calculated using the convolution between the inputs 𝑥[𝑛] and impulse response ℎ[𝑛]:

A. FIR (Finite Impulse Response)

Definition: FIR is a digital filter that has a finite impulse response. That is, ℎ[𝑛]=0 for all 𝑛 outside a certain interval.

General equation: 

Key features:

• Intrinsically stable.
• No feedback.
• Can be designed to have linear phase.
• Generally requires higher order than IIR for the same performance.

B. IIR (Infinite Impulse Response)

Definition: IIR is a digital filter that has an infinite impulse response. This is because of the feedback element in the filter structure.

General equation: 

Key features:

• Has feedback, so the impulse response is never truly zero.
• Can be very efficient in terms of order.
• Potential to be unstable if not designed properly.

4. Comparison of Impulse Response: FIR vs IIR

FIR:

• The impulse response stops after a discrete number of steps.
• The shape of the impulse response can be controlled directly through the coefficient 𝑏𝑘
• It is suitable for applications that require linear phase or constant delay.

IIR:

• The impulse response lasts forever (in theory).
• The response form is determined by both the input coefficients 𝑏𝑘 and the feedback 𝑎𝑘.
• More suitable for applications that demand high efficiency or have limited computing resources.

5. Frequency Representation and Transfer Function

The LTI system can also be represented in the frequency domain using the Z-transform.

FIR: 

• Only has zeros in the Z domain
• Has no polish except at 𝑧=0.

IIR:

• Has zeros and poles.
• Pole positions determine filter stability: all poles must be inside the unit circle for stability.

6. System Stability: Determining Factors

• FIR is always stable if its coefficients are finite.
• IIR can be unstable if there are poles outside the unit circle (|z| > 1).
• Therefore, IIR design requires extra attention to pole location.

7. Applications and When to Use FIR or IIR?

Use FIR when:

• Linear phase is required (e.g. in data communications and digital imaging).
• Stability without pole analysis is required.
• The system has sufficient computing power.

Use IIR when:

• Computational efficiency (low order) is required.
• The system has limited memory.
• Phase is not a major consideration (e.g. in audio filtering).

Simple Implementation Example (Python)

from scipy.signal import lfilter

# FIR filter dengan koefisien [0.2, 0.2, 0.2, 0.2, 0.2] (moving average)

b_fir = [0.2]*5

a_fir = [1]

# IIR filter sederhana (low-pass Butterworth orde 2)

from scipy.signal import butter

b_iir, a_iir = butter(2, 0.25)

# Sinyal input contoh

import numpy as np

x = np.random.randn(100)

# Output FIR dan IIR

y_fir = lfilter(b_fir, a_fir, x)

y_iir = lfilter(b_iir, a_iir, x)

Conclusion

Understanding the relationship between digital filters, impulse responses, and FIR and IIR filter types is very important in the world of signal processing. Some important points that can be concluded:

• Impulse response is key in understanding how a system processes signals.
• FIR has a finite impulse response, is easy to control, and is stable.
• IIR has an infinite impulse response, is more efficient in some cases, but requires attention to stability.
• The choice between FIR and IIR depends on application needs, resource constraints, and system design specifications.

By understanding this basic theory, an engineer or researcher can be wiser in designing an efficient and appropriate filter system.