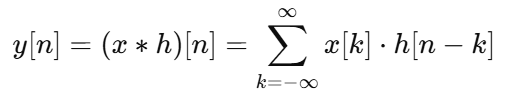Getting to Know LTI Systems: Convolution, Superposition, and Time Invariance in Full
Linear Time-Invariant (LTI) systems are an important foundation in engineering, particularly in signal processing, system control, and communications. Understanding LTI systems means understanding how modern digital electronics and algorithms work—from speech processing in smartphones to digital filters in audio.
In this article, we will dive into three core concepts in LTI systems:
1. Convolution
2. Superposition Principle (Linearity)
3. Time Invariance
1. What is an LTI System?
An LTI system is a system that has two main characteristics:
- Linearity (follows the principle of superposition)
- Time-Invariant (does not change with time shift)
If a system has both of these properties, then we can use very powerful mathematical tools such as convolution to analyze and predict the system's response to various inputs.
2. Principle of Superposition (Linearity)
Definition:
The principle of superposition states that if a system responds to input 𝑥1(𝑡) with output y1(t) and respond x2(t) with y2(t) then for combined input ax1(t)+bx2(t) the output is ay1(t)+by2(t).
Mathematically:
Simple Explanation:
A linear system does not "mix up" inputs in a complex way. The output is simply a sum and scalar product of previous outputs.
Real Example:
Think of an audio system: if you play two songs simultaneously, and your speaker system is linear, then the resulting sound you hear is a combination of the two songs, without any unexpected distortion.
3. Time Invariance
Definition:
A system is called time-invariant if a shift in input over time results in a shift in output in the same amount of time.
Mathematically:
if
Conceptual Explanation:
That is, the characteristics of the system do not change over time. The system "behaves the same" to inputs no matter when they are given.
Example:
A signal processing system that amplifies a signal by 2x is time-invariant if any sound signal, whether given at 10am or 10pm, is amplified 2x with identical results (time-shifted to reflect the input).
4. Convolution: A Key Tool in LTI Systems
Definition:
Convolution is a mathematical operation that describes how an LTI system responds to an input based on its impulse response.
Continuous Convolution Formula:
Discrete Convolution Formula:
Intuitive Explanation:
Convolution is "the way a system responds to an input signal" by summing the responses to each part of the signal. In an LTI system, the output is the sum of all the responses to the parts of the input, each delayed and multiplied by a certain weight.
Impulse Response:
The impulse response
ℎ(𝑡) is the system output when given input in the form of a delta function δ(t). This is the "characteristic" of the LTI system.
5. Simple Illustration of Convolution
Imagine throwing pebbles into a pond. Each pebble creates a ripple. If you throw two pebbles, the ripples will overlap.
- Input = time and force of the throw
- System = pond
- Output = ripple pattern that is formed
The total ripple is the sum (convolution) of the ripples of each pebble. That's how the LTI system works.
6. Why Are LTI Systems Important?
LTI systems are analytical, predictable, and stable. This makes them a vital tool in many applications:
- Digital filtering (DSP): Shaping sound, images, or signals to correct or modify information.
- Automatic control: For example, cruise control in cars or robotic systems.
- Communications: Modulating and demodulating signals.
- Non-linear systems: their response can involve exponents, logarithms, or complex functions of the input.
- Non-time-invariant systems: such as adaptive systems that change their behavior depending on time.
- Superposition ensures that the system is linear and can be analyzed using mathematical techniques.
- Time invariance makes the system consistent in time.
- Convolution provides a systematic way to find the output of the system for arbitrary inputs.
Post a Comment